If you haven’t heard this already, Pringles chips are the shape of a hyperbolic paraboloid.
pringles are actually just hyperbolic paraboloids .. really make u think pic.twitter.com/8rxW1LY0He
— Mr. Nomer (@Trivial__) September 11, 2019
What does that mean? Well, I don’t really know. All I know is that it’s one of those factoids I’ve stumbled upon on Twitter a handful of times, and while I appreciate the Snapple-fact trivia of it, my math-impaired brain can’t do anything more with that information. I know that Pringles are a hyperbolic paraboloid, I get that, but I don’t know what a paraboloid is or what exactly is so hyperbolic about it.
To try to make some sense of this for me, I’ve turned to three mathematicians who didn’t sleep through much of their high school math classes.

On Hyperbolic Paraboloids
Theron Hitchman, Professor of Mathematics at the University of Northern Iowa: Usually, the way mathematicians talk about this kind of thing is in an equation, but I think equations tend to scare people off, so, I guess you could say that a hyperbolic paraboloid is a kind of surface that, when cut one way, it looks like parabolas opening down, and if you rotate it 90 degrees, it looks like parabolas opening up.
On What a ‘Paraboloid’ Is
Varun Vachhar, software engineer: So, mathematically speaking, a parabola is a two-dimensional arc.
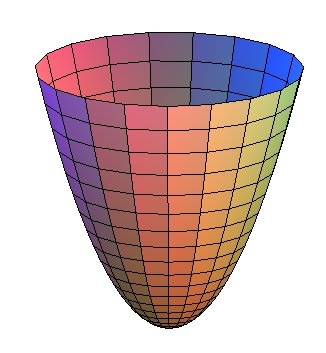
As for a paraboloid, that would be the three-dimensional version of that, where you’d rotate that arc to create a bowl-like structure.
On What ‘Hyperbolic’ Means
Matt Zaremsky, professor of mathematics at the State University of New York at Albany: “Hyperbolic” is an adjective that gets applied to all sorts of stuff that generally means that things splay outward like crazy. It technically means that it’s a space where things will deviate to a large degree, as the edges of a Pringle would.
On Other Hyperbolic Paraboloids
Zaremsky: A horse’s saddle is also a hyperbolic paraboloid. In fact, I think, if someone were to ask me what shape a Pringle was, I’d say “saddle-shaped,” just because hyperbolic paraboloids don’t come up that often. I don’t know, maybe some calculus professors are sitting around contemplating hyperbolic paraboloids all the time, but I’m not.
Vachhar: Hyperbolic paraboloids are really interesting. They’re my favorite shape actually, and aside from Pringles, they’re used a lot in architecture because they’re structurally really strong. Many shapes struggle with compression. A flat roof, for example, might buckle from too much weight, but with a hyperbolic paraboloid, the curves prevent buckling, just like how an arch is stronger than a straight beam.

On Pringles
Hitchman: The fact that Pringles are hyperbolic paraboloids is kind of a standard thing that people who teach multivariable calculus tell their students. Pringles have been around long enough to where teachers use them as a visual reference. Since American students will have seen Pringles, they’re often referred to when hyperbolic paraboloids are introduced.
On Why Hyperbolic Paraboloids Make for Good Chips
Hitchman: Pringles are all the same shape, which is part of the reason why they stack so well — there’s a uniformity to them — but them being hyperbolic paraboloids means they don’t move either, they fit nice and snug. Discs could spin or slide off of each other, but this shape nests together nicely.
On Their Favorite Type of Pringle
Hitchman: I just like the regular Pringles, but in my house, my wife usually gets to them before I do.
Vachhar: I live in Canada, so my favorite chip is “all dressed,” but for Pringles, I like ketchup-flavored.
Zaremsky: I really don’t like sour cream and onion, but that’s true for any chip. I just like the regular Pringles. Any time I’d go to my grandma’s house, I used to get Oreos and Pringles.
On Other Geometrically Interesting Foods
Hitchman: One food that’s geometrically cool is romanesco broccoli, because it looks kind of fractal-y. Fractals are shapes that repeat themselves on smaller and smaller scales, and they’re something that mathematicians study, though the ones on romanesco broccoli aren’t true fractals because nothing on earth is exactly a fractal.

Vachhar: Fortune cookies are really interesting. It’s similar to a Pringle where you start out with a disc and bend it in two different directions. I don’t think there’s a geometrical name for the shape of a fortune cookie though.
Zaremsky: While not exactly, an egg is interesting because it’s almost an ellipsoid.

On Which Shape Tastes Best (and Why)
Vachhar: I’ll say triangles because whenever you watch celebrity chefs, they always seem to say that triangles plate better than other shapes.
Zaremsky: Hexagon, because of honeycombs.
Hitchman: Definitely a torus. It’s the shape of a donut!


